Lesson 2
1. Lesson 2
1.4. Explore 3
Module 2: Trigonometry
Example 1: Equations of the Form cos θ = k, Where −1 ≤ k ≤ 1
Nasreen has been asked to solve the equation cos θ = −0.45 to the nearest degree. She knows that there must be two solutions to this equation.
Solution
Step 1: Nasreen determines the first solution by entering cos−1(−0.45) in her calculator and rounds it to the nearest degree.

Step 2: She sketches the angle given by her calculator (117°).
She knows that the terminal arm of the second solution, θ2, must be a reflection in the x-axis of θ1’s terminal arm. Therefore, she sketches θ2 with its terminal arm in quadrant 3.
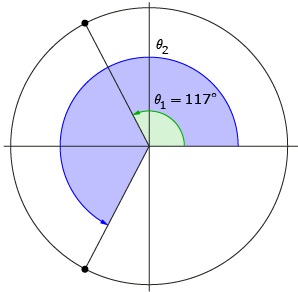
Step 3: Nasreen knows that a straight line is an angle of 180°; thus, the angle between θ1’s terminal arm and the x-axis must be 180° − 117° = 63°.
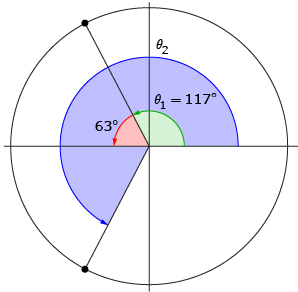
Step 4: Because the terminal arm of θ2 is a reflection in the x-axis of θ1’s terminal arm, Nasreen knows the angle between the x-axis and θ2’s terminal arm must also be 63°.
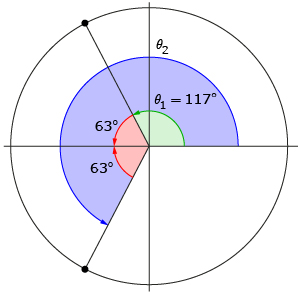
Step 5: Nasreen determines the second solution:
θ2 = 117° + 63° + 63° = 243°
The two solutions to the equation cos θ = −0.45 are θ1 = 117° and θ2 = 243°.