Lesson 3
1. Lesson 3
1.2. Explore
Module 2: Trigonometry
Explore
In Discover you determined the cosine, sine, and tangent for 0°, 90°, 180°, 270°, and 360° angles using points on a circle with a radius of 2. In Share 1 you may have discussed the fact that the values for these trigonometric ratios are always the same and don’t depend on the radius of the circle.
Finding the trigonometric ratios for these angles was straightforward because the terminal arms of each angle landed on either the x- or y-axis, making the point P(x, y) easily known. But what about other angles whose terminal arms do not lie on the x- or y-axis?
You already saved Module 2 Glossary Terms in your course folder. In this lesson you will define the following terms, and maybe others, in your copy of Module 2 Glossary Terms:
- 45-45-90 special triangle
- 30-60-90 special triangle
In the following activities you will investigate special triangles and explore how they can help identify trigonometric ratios for angles that do not lie on the x- or y-axis.
Try This 2
Follow the steps and answer the questions.
Step 1: Consider a square of side length 1 unit.
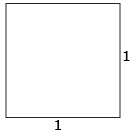
Step 2: When a diagonal is drawn in the square, what are the angles θ1 and θ2? ![]()
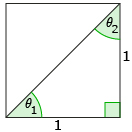
Step 3: The diagonal splits the square into two right triangles. What is the length of the hypotenuse? ![]()
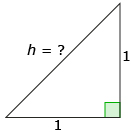
Step 4: Your diagram should now look like this:
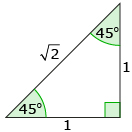
Step 5: Use this triangle to determine cos 45°, sin 45°, and tan 45°. ![]()
![]() Save your responses in your course folder.
Save your responses in your course folder.