Lesson 3
1. Lesson 3
1.4. Explore 3
Module 2: Trigonometry
Special Angles Around a Circle
Recall the question posed in Focus. Historically, how did mathematicians and engineers solve trigonometric equations without calculators or other forms of modern technology? The answer is that they used special triangles!
These two special triangles (45-45-90 and 30-60-90) were used by trigonometric table makers to determine the exact trigonometric values for all the angles shown in the diagram.
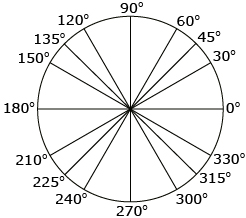
Other techniques, including trigonometric identities, were used to add more angles to their tables. These developments will be discussed in Mathematics 30-1.
For convenience, you often use a calculator to find the sine, cosine, or tangent of an angle. The resulting answer is often given as a decimal, which is an approximation of the value rather than the exact answer. For some special angles, you can find the exact answer as a fraction or a radical.
Take, for example, cos (30°) = 0.866 025 403. This is an approximation to cos (30°). The exact value can be found using the special triangle and is ![]() which is not a finite decimal.
which is not a finite decimal.
You can find the exact value when the angle is 30°, 45°, or 60°.