Lesson 3

Finding Angles from a Point on the Terminal Arm

 

In Try This 1 you were given the coordinates of endpoints on terminal arms of 0°, 90°, 180°, 270°, and 360° angles and asked to determine the cosine, sine, and tangent of these angles. This process can be extended to other angles where a point on the terminal arm of the angle is known. Consider the following example.

 

Point P(−2, 3) is on the terminal arm of an unknown angle, θ. Determine the exact values for cos θ, sin θ, and tan θ.

 

The first step is to draw a picture.

 

 

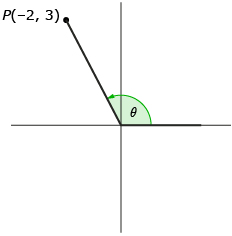
Recalling the primary trigonometric ratio definitions, you can write the following ratios:

 

 

The only piece missing is r, the distance from the origin to P(−2, 3). This can be determined by imagining that the terminal arm is the hypotenuse of a right triangle.

 

 

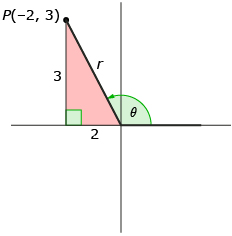
The Pythagorean theorem can be used to determine r.

 

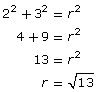
The primary trigonometric ratios of this angle can now be written in full.

 

 

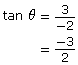Note that and are mathematically equivalent. By convention, the negative sign is normally written with the numerator.

 

Self-Check 2