Lesson 3

Lesson 3 Summary

 

In this lesson you investigated the following question:

• How can the cosine, sine, or tangent of an angle be determined without technology?

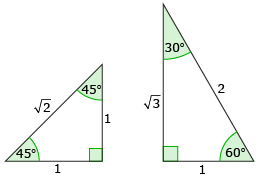
You learned how to determine the side lengths of 30-60-90 and 45-45-90 special triangles and how using triangles can be used to determine the cosine, sine, and tangent for each of the following angles.

 

 

 

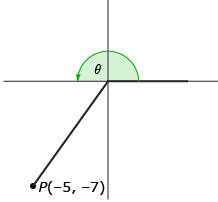
You also learned how to determine the exact values of cosine, sine, and tangent in situations where you only know the coordinates of a point on the terminal arm.

 

 

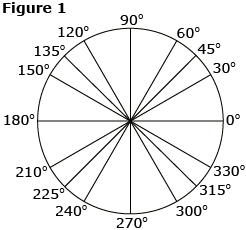
You don’t have to memorize the exact values for cosine, sine, and tangent for all sixteen angles shown in Figure 1.

• The values for 0°, 90°, 180°, 270°, and 360° can be easily determined using the coordinates of any point on their terminal arms.
  
  
• The values for 30°, 45°, and 60° can be determined using the special triangles shown above.
  
  
• All other values can be determined by using either 45-45-90 or 30-60-90 special triangles.

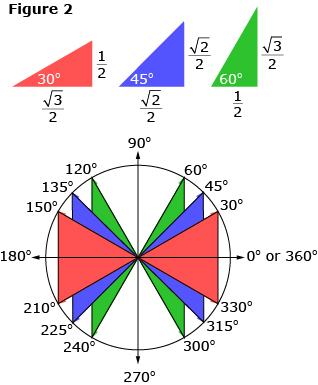
Another way to remember the ratios is to remember the red, blue, and green triangles.

 

The special triangles, 30-60-90 and 45-45-90, can be drawn in the unit circle, as shown in Figure 2. Knowing the ratios of the special triangles will determine the exact value of sin θ and cos θ and thus the x- and y-coordinates that lie on the edge of the circle.