Lesson 4
1. Lesson 4
1.3. Explore 2
Module 2: Trigonometry
Using the Sine Law to Solve for Distance

iStockphoto/Thinkstock
This is a photo of a trig point at Old Man of Coniston in England.
The sine law is valid for all triangles, but the law is especially useful for oblique triangles. This is because the sine law is the first formula you have encountered that is valid for oblique triangles and not all problems involve right triangles.
Trigonometry using oblique triangles was important in the early twentieth century when the British government wanted its maps (based on survey work done between 1783 and 1853) to be more accurate. The triangulation method of surveying was used to complete the Retriangulation of Britain between 1935 and 1962.
Concrete pillars called trig points were created all around the country. These pillars became the vertices of triangles that were used to create accurate maps of Britain. Trigonometry played an important role in helping to calculate the angles and distances between trig points.
Example 1: Lake Claire
Today, if you were to use triangulation to measure distances around Lake Claire in northeast Alberta, you might end up with trig points and corresponding triangles in the locations shown in the diagram.
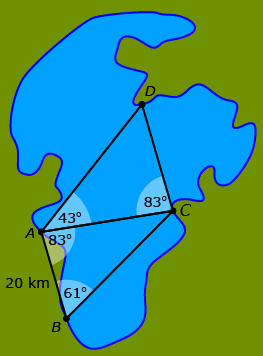
The sine law could be used to determine all the unknown distances. The following steps show the calculation of the distance across the lake, ![]() using
using ![]()
![]() is the only known side. Thus, to use the sine law, the angle opposite
is the only known side. Thus, to use the sine law, the angle opposite ![]() must be calculated.
must be calculated.
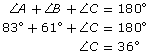
Write the sine law using a side-angle pair that you know and the side-angle pair with your unknown distance.
![]()
Multiply both sides by sin 61° in order to isolate ![]()
![]()
Cancel sin 61° to isolate ![]()
![]()
![]() = 29.7598…
= 29.7598…
Unless stated otherwise, distances should be rounded to the nearest tenth.
![]() = 29.8 km
= 29.8 km
Canada’s First Nations people were the first map makers in Canada. Undoubtedly, their maps were useful to the early European explorers in what would become Canada. However, these maps had two significant differences to what the Europeans would have been used to:
- The First Nations’ maps were usually memorized and only drawn when required to communicate locations and distances with others.
- The scale of First Nations’ maps often corresponded to travel times rather than absolute distances. As a result, two identical real-world distances would not be identical on the map if one route required more travel time due to rough terrain.
Self-Check 1
- Determine the length of
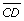 in Example 1: Lake Claire. Answer
in Example 1: Lake Claire. Answer
- Complete question 15 on page 110 of the textbook. Answer