Lesson 5

Explore

 

David and Jennifer don’t have enough information to use the sine law. However, there is another formula, the cosine law, which is also valid for any triangle.

 

The cosine law is usually written in the following way:

 

a2 = b2 + c2 − 2bc cos A

 

Recall from Lesson 4 that mathematicians typically label sides with lowercase letters and angles with uppercase letters. Furthermore, sides and angles with the same letter are across from one another. For instance, side a is across from ∠A.

 

 

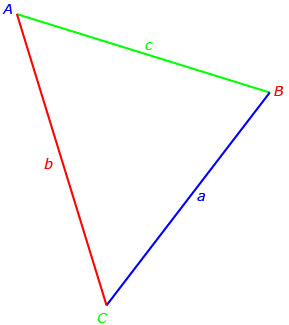
Keep this naming convention in mind. The variable, A, in the equation must be the measure of the angle across from side a, which is the measure you’ll be trying to determine. Look closely at the equation a2 = b2 + c2 − 2bc cos A. In order to determine the length of side a in the equation, you must know the

• lengths of the other two sides (b and c)
  
  
• angle across from the side you are trying to determine (A)

Try This 1

 

Use Cosine Law Explorer to see if the cosine law is valid for any triangle. Drag the vertices of the triangle, and confirm that the left side of the cosine law is always equal to the right side. Can you create a triangle where the cosine law will not work?

Save your response in your course folder.