Lesson 5

Read “Example 2: Determine an Angle” on page 117 of the textbook. Notice the two methods for using the formula.

• In Method 1, values are substituted directly into the formula.
  
  
• In Method 2, the formula is rearranged before the values are substituted.

Many students prefer Method 2—substituting values after the formula has been rearranged. As shown in your textbook, the rearranged form is

 

 

Self-Check 3

 

Given the following triangle, state three different ways the cosine law can be written when all three sides are given and you are solving for unknown angles. Answer

 

 

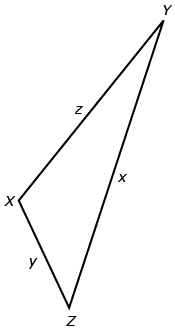
Try This 2

 

Rahim is learning how to use a compass in an orienteering course. He is standing at checkpoint C and knows distances to two other checkpoints, as shown in the diagram. In order to walk in the correct direction, Rahim needs to determine the angle between checkpoints A and B (∠θ on the diagram).

 

 

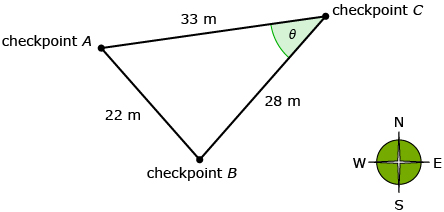
Rahim used the cosine law to determine ∠θ. Each step he used is described below. Write the mathematical formula or calculation described in each of the steps. Use the hints if you are stuck or if you need to check your progress.

Step 1: Write a correct version of the cosine formula.

 

Step 2: For this problem, ∠θ is across from the side that is 22 m long. Rahim replaces C in the formula with θ because that’s how the angle is labelled in his diagram. Then Rahim substitutes all the variables for values from the triangle.

 

Step 3: Rahim calculates what cos θ is equal to using his calculator.

When entering fractions on a calculator, extra care must be taken with brackets. The easiest approach is to always put the numerator in brackets and the denominator in brackets.

 

For this example, you would enter the following in your calculator:

 

(332 + 282 − 222)/(2(33)(28))

Step 4: Rahim uses his calculator to find θ.

 

Step 5: Rahim remembered to round his answer to the nearest degree.

 

 Save your responses in your course folder.

 

Self-Check 4

 

After you answer the questions, make sure you check the suggested answers carefully to ensure you understand the solution process. If you are still having trouble, contact your teacher.

Complete questions 2.a., 2.c., 5.c., and 17 on pages 119 to 122 of the textbook. Answers

Add both forms of the cosine law to your copy of Formula Sheet.