Lesson 5

Lesson 5 Summary

 

In this lesson you learned that although the sine law is valid for all triangles, sometimes you are not given enough information to use the sine law.

 

You also learned the cosine law, which is valid for all triangles (just like the sine law):

 

a2 = b2 + c2 − 2bc cos A or

 

When deciding whether to use the sine law or the cosine law, consider which values are given and which values you need to find.

• If you have a side-angle pair (i.e., one side and its opposite angle), then you can use the sine law.
  
  
• If you do not have a side-angle pair, then you will likely need to use the cosine law.
  

If you think back to the obstacle course in the Focus section, David and Jennifer did not have a side-angle pair. Therefore, the cosine law was used to find the length of rope needed.

 

 

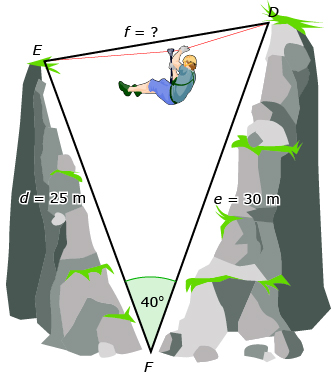
For a summary review of how to come up with the cosine law, watch “Law of Cosines” from the Khan Academy.