1. Lesson 1

1.8. Explore 3

Mathematics 20-1 Module 4

Module 4: Quadratic Equations and Inequalities

 

Graphing Quadratic Functions

 

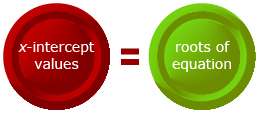
You have discovered that the roots of a quadratic equation can be found by determining the x-intercepts of the graph of the corresponding quadratic function. The x-intercepts are also known as the zeros of the quadratic function.

 

There are many ways of graphing a quadratic function. You can graph by hand with paper and pencil, or you can graph electronically using a graphing calculator, spreadsheet, or other graphing application.

 


textbook

Turn to “Example 1” on pages 208 to 209 of the textbook to see three different ways of graphing a quadratic function. As you work through the example, try to answer the following questions:

  • How can you tell how many roots there are by looking at the graph?

  • Which graphing method do you prefer?
Self-Check 2

 

This is a play button that opens Do You Know Your Quadratic Equations?

Complete Do You Know Your Quadratic Equations?

 


 

Number of Roots and Number of x-Intercepts

 

If the roots of a quadratic equation are equal to the values of the x-intercepts on its graph, it is reasonable to state that the number of roots is equal to the number of x-intercepts.

 

This is an illustration showing that the number of x-intercepts is equal to the number of roots of the equation.

 

Try This 3

 

  1. How many x-intercepts can a quadratic function have? Use Quadratic Functions to answer this question.

     
    This is a play button that opens Quadratic Functions.
    Screenshot reprinted with permission of ExploreLearning.


  2. What is the minimum number of roots that a quadratic equation could have? What is the maximum number of roots?

  3. Using Quadratic Functions from question 1, choose one quadratic equation for each of the different number of roots.

  4. Number your equations from question 3 and copy the equations into a document. Save your document as Questions_Your Name in your course folder. Record the roots of the equations in a separate document called Answers_Your Name.

course folder Save your work in your course folder.

 

Share 3

 

With a classmate, exchange your question documents from Try This 3 question 4. Use any graphing strategy to find the roots of each of the equations.

 

After you and your partner have completed each other’s question documents, exchange the documents again. Mark the questions using your answer document from Try This 3 question 4.

 

Discuss the following points:

  1. Did you and your partner have the same number of questions? Remember that you were asked to construct one question for each unique number of roots.

  2. What are the benefits and drawbacks of graphing by hand?

  3. For any quadratic equation with only one real root, what will its graph look like? What part of the graph intersects the x-axis?