Lesson 1
1. Lesson 1
1.12. Lesson 1 Summary
Module 4: Quadratic Equations and Inequalities
Lesson 1 Summary

In this lesson you investigated the following questions:
- How are the roots of quadratic equations related to the graphs of their corresponding quadratic functions?
- In what ways can you solve a quadratic equation by graphing?
You discovered that the roots of a quadratic equation are precisely the zeros of the corresponding quadratic function, which are, in turn, the x-intercepts of the graph. Therefore, you can solve a quadratic equation by finding the x-intercepts of the related quadratic function. You learned that any given quadratic equation can have one, two, or no roots depending on the number of x-intercepts.
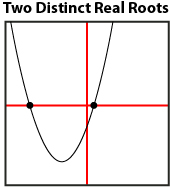
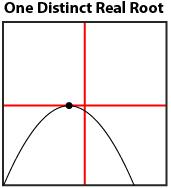
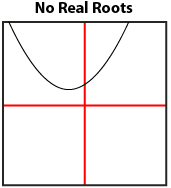
There are many ways of graphing a quadratic function. Besides constructing a graph by hand, you can graph electronically using spreadsheets, graphing calculators, or applets.
As an alternative to using the zero feature of a calculator to find the x-intercepts of a quadratic function’s graph, you can graph a related system of equations and determine the roots by finding the points of intersection.
The graphing methods you learned for solving quadratic equations can be used to solve any equation. It is still important that you know how to solve quadratic equations algebraically. Solving equations algebraically gives you a deeper understanding of the nature of these equations. This is the subject of the next several lessons.