Lesson 3

When you have an equation of the form (x − p)2 = q, it may be tempting to square the binomial and then collect like terms. For example:

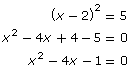
This method, however, overlooks the advantage of having the vertex form of the equation. Instead, by taking the square root of both sides of the equation, you will be within steps of determining the roots.

Turn to “Example 2” on page 237 of the textbook to see how you can solve a quadratic equation by completing the square. As you work through the solution, look for the answers to the following questions:

• To what form is the quadratic equation reduced in the very first step?
  
  
• Why is 25 added to each side?
  
  
• How are you supposed to solve ?

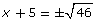Self-Check 1

Work through Completing the Square.

You have now learned how to solve quadratic equations of the form x2 + bx + c = 0 by following the steps in the table.

Step	Description	Example for the General Case
1	Complete the square.	x2 + bx + c = 0
2	Work with the squared expression.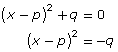
3	Square root both sides of the equation.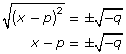
4	Isolate the root.

Notice that in the examples, a = 1. Now consider how you might apply the same process to solve quadratic equations in the general form ax2 + bx + c = 0, where a ≠ 1.

In Try This 3, you will again convert the general form into the form a(x – p)2 + q = 0 by completing the square. Pay special attention to what happens to a now that a ≠ 1.