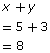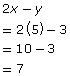Lesson 5

Solving a System of Equations by Graphing

 

Recall from your previous studies that to solve a system of equations means to find the values of the variables that will simultaneously satisfy all equations in the system. For example, consider the following system of linear equations:

 

x + y = 8

2x − y = 7

 

The solution to the equation is x = 5 and y = 3. This is because these values will satisfy each of the equations in the system. You can verify this by substituting the values into each equation as shown.

 

Equation 1: x + y = 8

 

LS	RS
	8

 

Equation 2: 2x − y = 7

 

LS	RS
	7

 

One way that you can solve a system of equation is by graphing. Recall that the points of intersection of the graphs of a system represent the solutions to the system.

 

Try This 2

1.  
   1. Solve the following quadratic systems by graphing. You may wish to do this using paper and pencil or using a graphing tool.
      
      
      1. 4x − y + 3 = 0
         2x2 + 8x − y + 3 = 0
         
         
      2. 2x2 − 16x − y = −35
         2x2 − 8x − y = −11
      
      Save a copy of your hand-sketched graphs or, if you used a graphing tool, by taking a screen capture of the completed graphs.
      
      
   2. Verify the solution by comparing the left side to the right side, as shown in the example before this Try This activity.
      
      
2. Retrieve your work from Try This 1. Compare your answers from the graphs in Try This 2 to those in Try This 1, Part A, question 1 and Try This 1, Part B, question 3. Do the graphs from this activity have a corresponding match in your earlier work? If not, make any necessary additions or revisions.

Save your work in your course folder.

---