Lesson 6

Turn to “Example 1” on pages 441 to 442 of the textbook. Without looking at the solution, try to solve the system on your own.

 

Two methods are presented as possible solution strategies: substitution and elimination. From Try This 2, you know that there are different approaches you can take within each of these methods. Work through the solution shown in the textbook. As you do so, focus on these questions:

• What reason is given for the solution strategy? For example, why is a particular variable selected for isolating or eliminating over the other variable?
  
  
• For the substitution method, how do you know which equation to substitute into once a variable is isolated?
  
  
• For the elimination method, which term is the target for elimination? Is it the squared term, the linear term, or the constant?

---

Self-Check 1

 

Complete Do You Know Your Linear-Quadratic Equations?

 

 

 

 

---

Using Differences to Solve Systems of Equations

 

Retrieve your work from Try This 1.

 

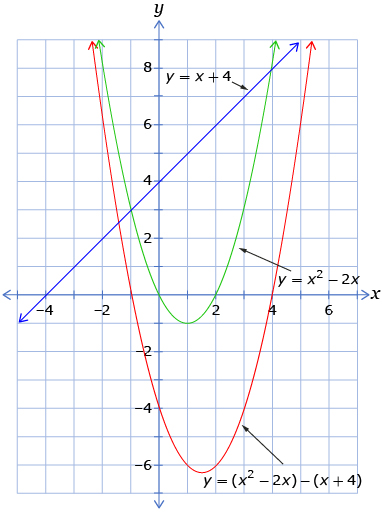
In that activity, you learned that you can also solve the system by graphing the difference of the equations.

 

y = x2 − 2x

y = x + 4

 

Compare your answer to Analysis question 7 to the following:

 

 

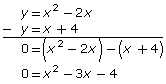
Look at your answer to Try This 1, Analysis question 6. Your graphs may look like the following.

 

Watch Graphing the Difference.

 

 

 

 

So, from an algebraic perspective, you must also be able to determine the solutions to the system by determining the roots of the difference of the equations. In this case, you could determine the roots of the equation x2 − 3x − 4 = 0. This can be done by any of several algebraic methods, such as factoring, square root strategies, or the quadratic formula.

 

Does this same idea apply to systems of quadratic-quadratic equations? You will find out in Try This 3.