Lesson 6

Lesson 6 Summary

 

In this lesson you investigated the following questions:

• Why do systems of equations yield the correct solutions even after they have been manipulated algebraically?

• Why is it important to be able to solve systems of equations algebraically as well as graphically?

You previously learned how to solve systems of linear-quadratic and quadratic-quadratic equations based on graphical methods. In this lesson you studied how to solve these systems using algebraic techniques. You used substitution and elimination strategies to manipulate the equations in each system. You learned that you can algebraically manipulate the equations in a system without changing the solutions. You verified this conclusion by graphing, as shown in the following graph from the Discover section of the lesson.

 

 

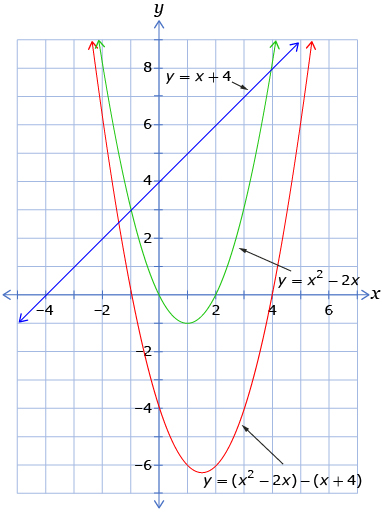
Knowing how to algebraically solve math problems, such as systems of equations, is an important skill for understanding math principles. While a graphical solution is often easy to obtain, such a solution process does not reveal the process by which the solution is obtained from a mathematical standpoint. Algebraic methods, when applied correctly, can take you step-by-step from problem to solution, which leads, in turn, to understanding and insight.

 

In the remaining lessons of this module, you will consider linear and quadratic inequalities, studying them from both a graphical and algebraic perspective.