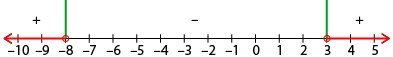1. Lesson 8

1.12. Lesson 8 Summary

Mathematics 20-1 Module 4

Module 4: Quadratic Equations and Inequalities

 

Lesson 8 Summary

 

This is an image of a futuristic environmentally friendly group of buildings.

© morganimation/12959959/Fotolia

In this lesson you investigated the following questions:

  • What principle is common to all strategies for solving quadratic inequalities?
  • How can you tell when a problem can be modelled by a quadratic inequality in one variable?

In this lesson you learned that quadratic inequalities in one variable can be solved in a number of different ways. Whether you solve quadratic inequalities in one variable graphically or algebraically, there is one principle that is common to them all. A quadratic inequality can be greater than 0 or less than 0, which means that the y-values are either positive or negative.

 

Therefore, regardless of the method you choose, you must determine solutions based on whether the y-coordinates in the solution are positive or negative. The following table summarizes how you determine the solution intervals based on signs.

 

 
Strategy for Solving How to Determine the Solution Interval(s)
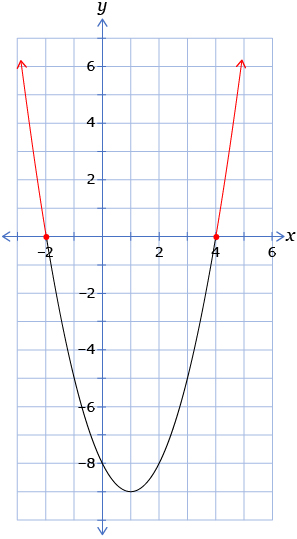
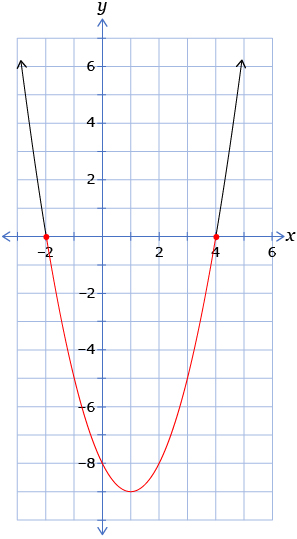
Graphing

Look above the x-axis if f(x) > 0 or f(x) ≥ 0.

 

This shows the graph of the parabola y = x squared – 2x – 8. It crosses the x-axis at (-2, 0) and (4, 0) and the y-axis at (0, -8). The parts of the curve above the x-axis are red.

 

Look below the x-axis if f(x) < 0 or f(x) ≤ 0.

 

This shows the graph of the parabola y = x squared – 2x – 8. It crosses the x-axis at (-2, 0) and (4, 0) and the y-axis at (0, -8). The parts of the curve below the x-axis are red.
Roots and Test Points

Use a test point from each interval to determine if the interval will yield positive or negative values of the function.

 

This is a number line with lowest value -10 and highest value 5. Open circles are shown at -8 and 3. A red arrow extends from -8 to the left and another red arrow extends from 3 to the right. The interval x < -8 is labelled as positive, the interval -8 < x < -3 is labelled as negative, and the interval x > 3 is labelled as positive.

 
Sign Analysis

Consider the signs of the factors at each interval. Select the solution interval(s) based on the signs of the product of the factors.

 

This is a table testing the regions into which the number line is partitioned by the inequality.

 
Case Analysis

Consider what the signs of the factors could be in order to satisfy the inequality based on the following four possible cases:

  • Case 1: (positive) × (positive)
  • Case 2: (positive) × (negative)
  • Case 3: (negative) × (positive)
  • Case 4: (negative) × (negative)

Then graph each possible case to determine the solution intervals.

 

You also modelled problems with quadratic inequalities in one variable. There are two conditions that are common to such problems. The first is that the situation can be represented by a quadratic function. The second is that the problem asks about points on the function that are greater than or less than a reference point.