Lesson 1
1. Lesson 1
1.8. Explore 4
Module 6: Rational Expressions
The Property of 1
What happens to a number if you multiply the number by 1? If you said that the number remains unchanged, you are absolutely right. This property of one is critical in determining equivalent expressions in mathematics.
Try This 3
- Multiply or divide the following numbers.
- Verify that the end result for each of the calculations in question 1 is equivalent. You may want to do this by using your calculator to check that the decimal representation of the original number is identical to that of the final number.
- To what number are

 and
and  equivalent?
equivalent?
- Compare the following two expressions:
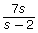 and
and 
- Identify the non-permissible value(s) for s in each expression.
- Are the expressions equivalent? How do you know?
- Identify the non-permissible value(s) for s in each expression.
![]() Save your responses in your course folder.
Save your responses in your course folder.
You will use your responses to question 1 to complete Share 2, Part B.
Generating Equivalent Rational Expressions
Turn to page 313 in the textbook. Read the section “Equivalent Rational Expressions” for an explanation of how to generate equivalent expressions. As you follow the process that takes a rational expression to an equivalent expression, think about how you could reverse the process.
How could you take the equivalent expression and convert the expression back to the original rational expression?
![]() Record your ideas in your course folder. You will look at this process again later in the lesson.
Record your ideas in your course folder. You will look at this process again later in the lesson.
Cross Multiplying to Confirm Equivalent Expressions
The product of any number and 1 is the number itself. Although the product may look very different, the product is, in fact, equivalent to the original number.
As revealed in Try This 3, to generate equivalent expressions, you simply multiply both the numerator and denominator by the same value.
To confirm that two expressions are equivalent, simply use the cross-product method.
If ![]() then ad = bc.
then ad = bc.
Here is the proof. Multiply both sides by the common denominator bd; then simplify the expression.

Therefore, if ![]() then ad = bc.
then ad = bc.