Lesson 1
Completion requirements
Created by IMSreader
1. Lesson 1
1.9. Explore 5
Module 6: Rational Expressions
Simplifying Rational Expressions
![]()
A good way to simplify rational expressions is to factor all second-degree polynomials. You can then check for factors common to both the numerator and the denominator.
To simplify a rational expression means to write an equivalent expression where the greatest common factor between the numerator and the denominator is 1. Such an expression is described as being in simplified form, or reduced to lowest terms.
The following example shows how you can simplify a rational number by using the method of prime factorization. Pay careful attention to the steps of this example. You will apply these steps to rational expressions in Try This 4.
Example
- Simplify
 by using prime factorization.
by using prime factorization.
- Verify that the simplified form is equivalent to the original rational number.
Solution
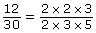
By rearranging the order of the factors in the numerator, the expression can be written as the product of three fractions.
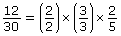
Since the first two fractions are equal to 1, the expression is simplified to

Therefore, according to the property of 1, where any number multiplied by 1 is equal to itself,
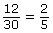
- You can use cross-products to verify that
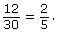
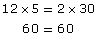
Since the cross-products are equal,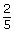 is equivalent to
is equivalent to 