Lesson 1

 Turn to “Example 3” on page 315 of the textbook to see how you can simplify a rational expression consisting of two variables. As you work through the solution, answer these questions:

1. What methods are used to factor the numerator and denominator?
   
   
2. How are the examples of non-permissible values determined?
   
   
3. How do you determine an expression for the non-permissible values of y?
   
   
4. Which method do you prefer for completing part c? Why?

Save your responses in your course folder.

 

Self-Check 2

 

With a partner, play Simplify Rational Expressions. Each of you will answer a set of math questions. When you’re done, compare your answers. Your answers should match in each row. If your answers do not match, work together to figure out where you went wrong. Answer

 

Save your responses in your course folder.

 

Factoring the Numerator and the Denominator

 

When you encounter a rational expression where both the numerator and denominator must be factored before the expression can be simplified, it is likely that they will share a common factor. You can use this knowledge to factor more easily.

 

For example, suppose you are required to simplify the following rational expression:

 

 

Step 1: Start by factoring the simpler of the two polynomials in the numerator and denominator. In this case, factor the numerator.

 

           

Step 2: Since the numerator has a binomial factor of (x + 3), there is a chance that the denominator will also have the same factor. If so, you will have the following:

 

           

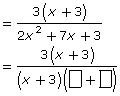
Step 3: By inspection, you can determine the terms of the second binomial factor.

 

                      

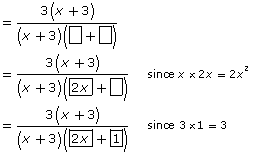
Step 4: You should check that 2x + 1 is the second factor by multiplying (x + 3)(2x + 1). In this case, the product is 2x2 + 7x + 3. Therefore, the correct factors are (x + 3) and (2x + 1).