Lesson 1
1. Lesson 1
1.13. Connect
Module 6: Rational Expressions
In the Lesson 1 Assignment you will demonstrate your understanding of the lesson outcomes. You will apply the concepts and strategies you learned to new situations. You must show your work to support your answers.
Open your copy of Lesson 1 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Project Connection
In Module 6 Project: Game Challenge, you will design and analyze games for a reality show. In the first phase of the project, you will research and brainstorm ideas for different games.
Go to Module 6 Project: Game Challenge. Read all parts of the Module 6 Project as an overview of what you will be doing to complete the project. Complete Step 1.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond
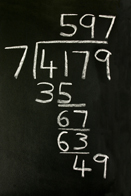
© Sharpshot/2754084/Fotolia
Do you remember how to divide numbers by long division? The image shows the long division of 4179 by 7. The quotient is 597. Study the image in order to review the process.
Did you know that you can also apply long division to polynomials?
In this lesson you simplified expressions, such as ![]() , by removing factors common to the numerator and the denominator. Long division is another method you can use to simplify rational expressions.
, by removing factors common to the numerator and the denominator. Long division is another method you can use to simplify rational expressions.
Part A
Compare the long division of rational numbers as shown in the image versus the long division of polynomials shown here:
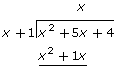
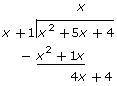
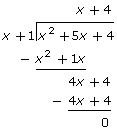
Answer the following questions:
- Where do you look for the simplified form of the original rational expression?
- Notice that the remainder is 0. What does that mean? What would it mean if the remainder were not equal to 0?
- Where do you look to find non-permissible values?
Part B
- Return to some of the questions you completed in this lesson. Use the method of long division to see if your answers match. Are there rational expressions that are better simplified with the long-division method? Are there expressions that are difficult to simplify with this method?
![]() Save your work in your course folder.
Save your work in your course folder.