Lesson 2

Turn to “Example 1” on page 324 of your textbook. This example shows a multiplication expression that is similar to the one you encountered at the end of Share 1. Work through the example to confirm your discussion in Share 1. Focus on the steps you would take, particularly the first step, to be able to efficiently multiply and simplify the product.

Try This 3

Retrieve your notes from Share 1. Multiply the expression given using the method presented in the example. You should obtain a constant of 2 if you simplify correctly. You should also obtain two non-permissible values.

Save your responses in your course folder.

Self-Check 1

Check your understanding of the concepts presented so far by completing Multiplying Rational Numbers Self-Check.

You have just learned how to multiply rational numbers. Recall that dividing rational numbers is a process that involves multiplying the first number by the reciprocal of the second number.

How does the division of rational expressions compare with the division of rational numbers? In Try This 4 you will explore both procedures.

Try This 4

1. Solve 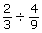without using your calculator.
   
   
2. Describe a procedure for solving 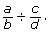You may want to revisit your answer to question 3 in the Are You Ready? section.
   
   
3. Apply the same procedure described in question 2 to determine the quotient of each of the following expressions:
   
   
   1. 
      
      
   2. 
      
      
4. How can you verify your answers to question 3?

Save your responses in your course folder.

Share 2

You can use a graphing calculator to check whether two expressions are equal. For example, you may wonder if is equal to Simply type the first expression into Y1 and the second expression into Y2. Remember to add brackets around each polynomial to maintain the original expression. If the two expressions are equal, the graphs will be the same. In some calculators, you can change the thickness of a graph so you can see more clearly that the two graphs are in fact identical.

Compare your results from Try This 4 with a partner, and discuss the following questions.

1. When dividing rational expressions, where should you look in order to determine the non-permissible values? Is it sufficient to look at the denominators only?

2. In question 3 you divided rational expressions that had a common denominator. Consider the expression 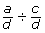. What is the result when the expression is simplified? Can you and your classmate uncover a pattern to describe a short cut that leads to the same answer?