Lesson 2

In your graph from Try This 4, the single critical point is found at x = 2. It is at this point that the graph of  changes direction. Notice that for all values of x greater than 2, the corresponding y-values on the graph are equal to x − 2. However, for all values of x less than 2, the corresponding y-values are equal to −(x − 2).

This leads to a new notation known as piecewise notation. You can use this notation to express as

It is called piecewise notation because it breaks the function into distinct “pieces.” Theoretically, you could break the function into as many pieces as you want. However, the generally accepted practice is to break the function into pieces at the critical points.

Turn to part d) of “Example 1” on pages 370–372 of your textbook to see how you can express in piecewise notation. As you read, focus on finding the answers to these questions:

• How was the value 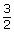 obtained?
• How does the negative in the expression −(2x − 3) affect the y-values when ?

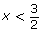Try This 5

Consider the function . Express the function using piecewise notation. (Access the hints if you need help.)

1. What do I do first?
   
   
2. How do I find critical points?
   
   
3. How do I use critical points?
   

Compare your final answer with the one in the textbook. You can find it on page 374, part d).

Self-Check 3