Section 1

Explore

 

In Discover you investigated the Rule of 72. You discovered that by using the Rule of 72, and given an annual interest rate that is compounded annually, you can estimate the time required for a given investment to double in value.

 

approximate number of years for the investment to double =

 

Example

 

During the ski season, Rose works as a ski instructor at Mont Tremblant in Québec. She has just invested $2000 of her savings at 4% compounded annually. Use the Rule of 72 to estimate the number of years it will take for Rose’s investment to double.

 

Solution

 

The annual interest rate = 4%

 

Use the Rule of 72:

 

Divide 72 by 4.

 

 

Rose’s investment will double in about 18 years.

---

You have seen the rule of 72 explained using the following formula:

 

approximate number of years for the investment to double =

 

But in Try This 1 you divided 72 by 9, which is the number of years it took the investment to double—not the interest rate! This is because the formula can be rearranged to estimate the annual interest rate if you know the doubling time for an investment.

 

interest rate as a percent =

 

 

---

In the next example you will explore how the Rule of 72 can be used to estimate the annual interest rate from the doubling time for an investment.

 

Example

 

Ron, who is 15 years old, loves snowmobiling. He has his eye on a model that costs $6000, and Ron would like to own the snowmobile by the time he turns 25. If he has $3000 in savings today, at what rate of interest should Ron invest the $3000 so that he will have $6000 in ten years?

 

Solution:

 

doubling time = 10 years

 

Use the Rule of 72:

 

 

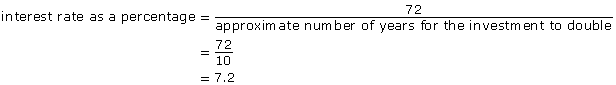
Ron should look for an investment that earns at least 7.2%.