Section 2

Explore

 

In Discover you used a specific applet to convert units through unit analyis. There are many ways to convert units.

• Use a specific applet, as you did in Discover.
  
  
• Harness the power of a search engine, like Google.
  
  
• Understand the calculations that are required and do these calculations yourself whenever or wherever you are.

Try This 2

Enter “36.11 m/s to ft/s” into the Google® search box.

 

 

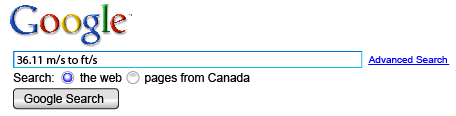
Google has a calculator that does these kinds of unit changes. How did the answer from Google compare with the answer from question 3 of Try This 1? Try converting 36.11 m/s to some other units of speed.

---

Unit Analysis Calculations

 

Conversions require some knowledge about how different measures are related to each other and how to multiply fractions. For example, to change metres/second to feet/second, you would do the following:

 

Step 1: Look up the conversion for metres to feet and find that 1 m = 3.280 839 9 ft. You might also have found the conversion to be either or . These are sometimes referred to as conversion factors. When you multiply by a conversion factor, you are really just multiplying by 1. Watch Conversion Factors to see the proof!

 

Step 2:  Determine what conversion factor you must use. The conversion factor with the metres in the denominator will allow you to cancel out the metres in the numerator of the original units, .

 

Step 3:  Multiply the factor, and cancel out units found in both the numerator and denominator.

 

 

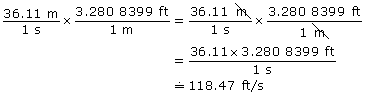
This three-step method is more work for you than using a search engine, but you can see exactly how the units change and you can do the conversion even if there isn’t a computer handy.

 

You may remember from Discover that some conversions take two or more steps. A conversion like 36.11 m/s = 80.775 769 5 mi/h requires many steps. You’ll notice that two units need to be changed—distance and time.