1. Section 2

1.7. Explore 2

Mathematics 20-3 Module 3

Section 2: Slope—Rate of Change

 

Self-Check 1
  1. Use one of the following conversion factors to show that 36.11 m/s = 1421.653 54 in/s.

     


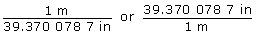
    Need help getting started? hint

    Answer

  2. Use the following information to show a calculation that converts 36.11 m/s into 80.775 769 5 mi/h.

    You can use the following conversion factors to help you:

    0.000 621 371 192 mi = 1 m

    3600 s = 1 h

    Need some help getting started? hint hint hint

    Answer

Did you notice that the m and the s disappeared in your calculations? Why did they disappear? hint

Many of the measurements in the lesson have had units that were made up of or showed a relation between two units. For example, in 36.11 m/s, the unit of metres has been related to seconds. When you write a ratio with two different units, it’s called a rate. In Try This 3 you will see how a rate is related to slope and how unit analysis can help some rate problems.

 

Try This 3


The skateboarder from the Discover section was moving at a speed of 36.11 m/s. How far could he travel in one minute?

  1. Calculate the answer by completing this chart. If the skateboarder has a speed of 36.11 m/s, then he must move a distance of 36.11 m every second.

    Time (s) Distance (m)
    0 0
    1 36.11
    2 72.22 = (36.11 + 36.11) or (36.11 × 2)
    3      = (36.11 + 36.11 + 36.11) or (36.11 × 3)
    • •
    • •
    • •
    59      = (36.11 × 59)
    60      = (36.11 × 60)

While this chart works, it is time consuming. You might prefer to graph a few points from the chart. You’ll be able to see the distance increase each second.

 

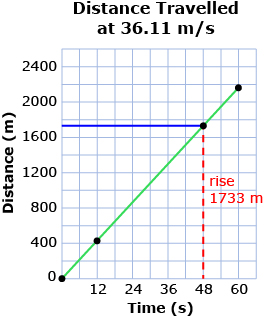
This graph shows the distance covered over a time of 0 to 60 seconds when the speed is 36.11 m/s.

 

Notice how the blue line in the graph helps. This line connects the point on the green line to the vertical axis at 48 s. This lets you read the value of the distance. The graph lets you get an answer of about 1733 m travelled in 48 s.

  1. What is the slope of the green line? hint

  2. How does an understanding of unit analysis help you figure out that the speed, 36.11 m/s, has to be multiplied by 60 s and not divided by 60 s to find the total distance travelled in 60 s? What would happen if you had divided by 60 s?

course folder Save your responses to your course folder.

 


How much time is used to travel 1733 m?
They disappeared because units that are the same in the numerator and denominator cancel each other out.

Convert seconds to hours like this.

 


Did you notice that the s disappeared in this calculation?

First, convert metres to miles like this.

 

 

 

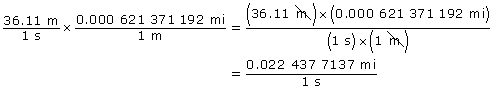
Did you notice how the metres cancelled and miles were left?

Do this as a two-step process. Perhaps start by changing metres to miles.

 

 


You complete the conversion by changing seconds to hours.

Begin like this: