Lesson 1

Did you identify three different scenarios in Identifying Right-Angled Triangles in Real Life that were represented by right triangles in three dimensions? If not, go back and watch the slideshow again or contact your teacher.

 

The following example looks at how you might solve a problem involving right triangles in three dimensions.

 

Example

 

A javelin is 2.2 m long. A wooden storage chest is 2 m long, 80 cm wide, and 50 cm high.

1. Show that this javelin cannot lie flat on the diagonal at the bottom of the chest.

2. Can the javelin lie diagonally from one corner at the bottom of the storage chest to the opposite corner at the top of the chest?

Solution

1.  
   

   Sketch and label your diagram. Let x be the diagonal distance across the bottom of the chest. The length of the bottom is 2 m. The width of the bottom is 80 cm or 0.80 m.
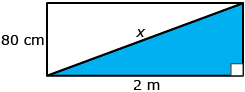
   Use the Pythagorean theorem to find x.   c2 = a2 + b2
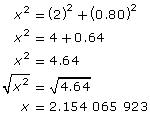
   Because the javelin is 2.2 m long, it cannot sit flat along the diagonal at the bottom of the storage chest, which has a maximum length of 2.15 m.	x ≅ 2.15 m

   
   
2.  
   

   Sketch and label your diagram.   The red triangle in this sketch can be used to find the diagonal through the centre of the storage chest. The legs are x and 50 cm long. The hypotenuse, d, is the diagonal distance through the centre of the chest.
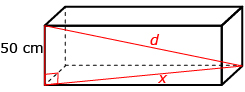
   In part 1, you found that x is about 2.15 m. As before, you need all the measurements to be in the same units.   Convert 50 cm to 0.50 m.
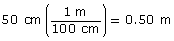
   Use the Pythagorean theorem to find d.   c2 = a2 + b2
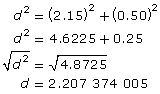
   The javelin is only 2.2 m long and, therefore, shorter than the diagonal of 2.21 m.   The javelin will fit in the storage chest.	d ≅ 2.21 m

   
   

Self-Check 2

 

In the javelin example, if one end is placed at one corner of the bottom of the storage chest, how high up along the opposite corner will the other end be? Round to the nearest centimetre. Answer

---