Lesson 4
Completion requirements
Created by IMSreader
1. Lesson 4
1.4. Discover
Module 4: The Right Kind Of Triangles
Discover
In Lesson 3 you used your clinometer to find the height of a totem pole or another pole, like a light standard. In the next Try This activity you will again look to find the height of a pole, but this time you will not be standing on the ground!
Try This 1
You are given the following diagram showing a flagpole outside a second-storey window. Use the information in the diagram to answer the following questions.
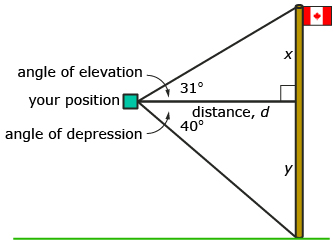
- In the diagram, there is one piece of information missing. What is needed before you can determine the height of the flagpole?
- How would you explain the steps involved in solving this type of trigonometric problem?
- Why were two triangles used to illustrate and solve this problem? Could the problem have been solved using one triangle? Explain your answer.
![]() Save your work to your course folder.
Save your work to your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or in a group.
- How did the strategy you used to solve this problem compare with others? Would you use the same strategy or change your strategy based on the discussion you’ve had?
- What are the similarities and differences between the problems in Try This 1 and the Try This 1 in Lesson 3, where you used your clinometer to find the height of a tall object?
![]() If required, save a copy of your discussion and your diagram in your course folder.
If required, save a copy of your discussion and your diagram in your course folder.