Lesson 1

Complete question 1 of “Build your Skills” on page 134 of the textbook to check your understanding of the surface area of a cylinder. Answer

In Try This 2 you saw that the surface area of a cylinder is made up of the area of its component pieces: two circles and a rectangle. These pieces can be examined using the net of the 3-D object. You will now explore the surface area of a rectangular prism and pyramid. Pay close attention to how the net is again used to find the surface area of these 3-D objects.

Try This 3

Use the Exploring Surface Area, Volume, and Nets applet in “Explore It” mode to help answer the following questions. Make sure you have selected “Surface Area” for the rectangular prism and rectangular pyramid before you begin.

1.  
   1. Use the applet to create a rectangular prism with a length of 6 m, a width of 5 m, and a height of 4 m. What is the rectangular prism’s surface area?
      
      
   2. Draw a net of this rectangular prism. How many faces are shown in your net?
      
      
   3. How many terms are there in the applet's calculation of the surface area? Relate each part of the surface area formula used in the applet, 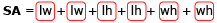, to the net you drew of this prism.
      
2.  
   1. Use the applet to create a rectangular pyramid with a length of 6 m, a width of 5 m, and a vertical height of 4 m. What is the rectangular pyramid’s surface area?
      
      
   2. What do k1 and k2 represent? Why wasn’t the height of the pyramid, 4 m, used directly in the calculation of surface area?
      
      
   3. Sketch a net of this pyramid. Include the dimensions.
      
      
   4. Relate each part of the surface area formula used in the applet,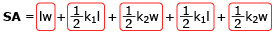, to the net you drew of this pyramid.

Save your answers to your course folder.

Share 2

Share your responses to the questions in Try This 3 with a classmate or with a group of people. Then refer specifically to the nets created in questions 1.b. and 2.c. as you discuss the following questions:

• What sides in a rectangular prism are identical? What sides in a rectangular pyramid are identical?
  
  
• How could your understanding of identical sides from the question above help simplify the formula for the surface area of a rectangular prism? How could the formula for the surface area of a rectangular pyramid also be simplified?

If required, save a copy of your discussion in your course folder.