Lesson 3
1. Lesson 3
1.5. Explore
Module 6: Surface Area
iStockphoto/Thinkstock
Explore
In Discover, you developed the formula for the surface area of a sphere and found that the surface area is exactly 4 times the area of a circle with the same radius.
In Explore, you will apply surface area formulas to solve a variety of problems. You will also manipulate these formulas to calculate dimensions of three-dimensional objects when given the surface area.

Photos.com/Thinkstock
Archimedes of Syracruse (287–212 BCE) was one of the greatest mathematicians and inventors of all time. Legend has it that he leapt from his bath crying “Eureka” (Greek for “I discovered it”) when he realized that the buoyancy of submerged objects could be used to determine whether the King of Syracruse’s crown was pure gold.
A brilliant and inventive mind, Archimedes considered his work with the sphere, including a proof of the formula for its surface area, his greatest accomplishment.
The following example gives you an opportunity to use the formula for the surface area of a sphere that you determined in Discover.
Example

iStockphoto/Thinkstock
An NBA basketball is approximately 24 cm in diameter. What is the surface area? Round your answer to the nearest cm2.
Solution
The diameter of the ball is 24 cm, but you need the radius for the surface area formula.
The radius, r, is equal to 24 cm ÷ 2, or 12 cm.
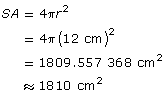
The surface area of the basketball is approximately 1810 cm2.