Lesson 4

Discover

 

In Launch you reviewed how the area of two-dimensional shapes changed when their linear dimensions increased or decreased by a factor. You may have noticed the following:

• If you doubled the length and width of a rectangle, its area increased 22, or four, times.
  
  
• If you tripled the dimensions in a parallelogram, its area increased 32, or nine, times.
  
  
• If you increased the radius of a circle by a linear factor of 5, its area increased 52, or 25 times.

Does changing the linear dimensions have the same effect on surface area as it does on area?

---

In Try This 1 you will investigate how changing the linear dimensions (length, width, and height) of three-dimensional objects changes their surface area.

 

Try This 1

 

How does the surface area of a cube change when its dimensions are doubled, tripled, or quadrupled?

 

Step 1: Click on the button to the left to open the “Exploring Surface Area, Volume, and Nets – Explore It” applet. Choose the rectangular prism from the list of objects and make sure that “Surface Area” is selected. Create a cube with these dimensions: length = 1 m, width = 1 m, and height = 1 m. Review the calculation for the surface area and record the surface area in the third column of a chart similar to the one that follows.

 

Step 2: Double the dimensions of the cube—in other words, the dimensions are changed by a linear scale factor of 2. The new dimensions should be length = 2 m, width = 2 m, height = 2 m. Determine the surface area and record it in the chart.

 

Step 3: Change the dimensions of the original cube by a linear scale factor of 3. In other words, triple each dimension of the original cube. Determine the surface area and record this information in the chart.

 

Step 4: Change the dimensions of the original cube by a scale factor of 4. Determine the surface area and record this data in the chart.

 

Change to Dimensions	Linear Scale Factor	Actual Dimensions	Surface Area	Surface Area Scale Factor
Original	1	1 × 1 × 1
Double	2	2 × 2 × 2
Triple	3
Quadruple	4

 

Now, based on your investigation, answer the following questions.

1. Calculate the surface area scale factor for each change in cube dimensions by using the following formula.
   
   
   
   
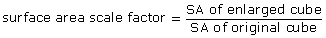
2. What is the relationship between the linear scale factor and the surface area scale factor?
   
   
3. Based on the relationship you identified in question 2, answer the following questions.
   
   
   1. If the cube’s dimensions increased by a linear scale factor of 10, by what scale factor must the surface area of the cube increase?
      
      
   2. If the cube’s dimensions increased by a linear scale factor of k, by what scale factor must the surface area of the cube increase?
      
      
4. Are you surprised by what you found? A cube has three dimensions—length, width, and height—but the linear scale factor is squared, not cubed, to find the surface area scale factor. Use an example to explain why this happens.

Save your responses in your course folder.

 

Share 1

 

Share your responses to the questions in Try This 1 with a classmate or with a group of people.

 

If required, save a copy of your discussion in your course folder.