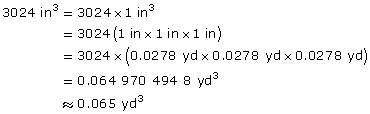Lesson 4
1. Lesson 4
1.6. Explore 2
Module 7: Volume and Capacity
As you read through the following examples, think of different ways in which the composite figures could have been divided.
Example
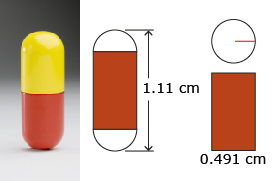
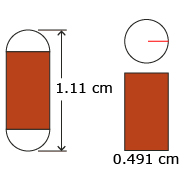
A gelatine capsule containing medication is 1.11 cm in overall length and 0.491 cm in diameter. This capsule is a composite figure made up of a cylinder with two hemispherical ends. What is the capsule’s capacity in millilitres? Round your answer to two decimal places.
Note: A hemisphere is half a sphere, and 1 mL = 1 cm3.
Creatas Images/Thinkstock
Solution
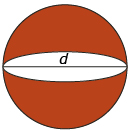
The two hemispherical ends form one sphere with a diameter of 0.491 cm.
Creatas Images/Thinkstock
The radius, r, of the sphere and of the cylinder is one-half the diameter, d.
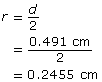
Find the height, h, of the central cylinder.
Creatas Images/Thinkstock

Find the total volume of the capsule.
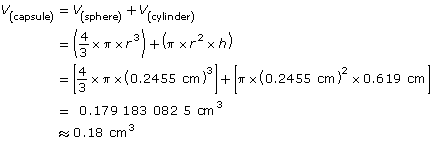
Because 1 mL = 1 cm3, the capacity of the capsule is about 0.18 mL.
Example
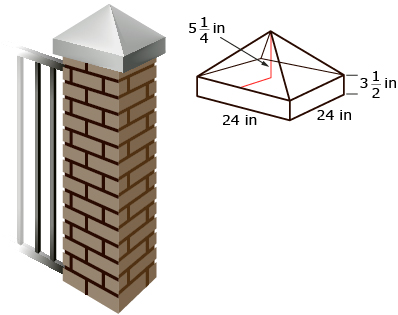
Consider the pillar shown.
- How much concrete is needed to make the top piece of the brick pillar?
- Concrete is sold in cubic yards. Convert the volume to cubic yards. Round your answer to three decimal places.
Solution
- The total volume of the pillar is made up of the volume of the rectangular (square) prism and the volume of the square pyramid (tetrahedron).
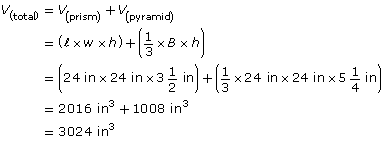
The volume of concrete needed is 3024 in3.
- To convert inches to yards use 1 in = 0.0278 yd.