Lesson 5

Explore

 

Architects need to know the effect of scale factor on volume when they make scale models of buildings. When doubling the dimensions of a flowerbed, gardeners need to know the effect of the scale factor on the flowerbed’s capacity in order to purchase the correct amount of soil.

 

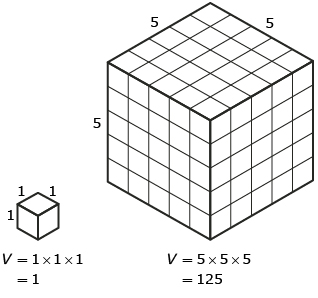
In Discover you examined the relationship between the scale factor—the number by which each dimension is multiplied—and the volume of a cube. You may have discovered this information:

• If one dimension changed by a factor of k, the volume changes by a factor of k.

• If two dimensions are changed by the same scale factor of k, the volume changes by a factor of k2.

• If all three dimensions are changed by the same scale factor of k, the volume changes by a factor of k3.

So, if you multiply each dimension of a cube, for instance, by a factor of 5, the volume of the new cube would be 53, or 125 times, more than the original cube.

 

 

Does this relationship apply to all three-dimensional figures?

 

Try This 2

 

Open Investigating the Volume of Cylinders to help you answer the following questions. When the scale factor is 1, the cylinder radius and height are both equal to 1 m.

 

1. Complete the following table. Some entries are filled in as examples.
   
   

   Scale Factor	Volume (in cm3) when   • only height   is multiplied by the linear scale factor	Volume (in cm3) when   • only radius   is multiplied by the linear scale factor	Volume (in cm3) when   • height • radius   are multiplied by the linear scale factor
   1 (original cylinder)	1	1	1
   2
   3
   4
   5
   k

   
   
2. How is the volume affected if only the height is multiplied by a scale factor of k?
   
   
3. How is the volume affected if only the radius is multiplied by a scale factor of k?
   
   
4. How is the volume affected if both the radius and height are multiplied by the scale factor of k?
   
   

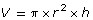5. The formula for the volume of a cylinder is . If the cylinder height is increased to 2h but the radius remains the same, the new volume becomes 2V.
   
   

   That fact can be shown as follows:
   
   
    
   
   
   
    
   
   
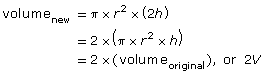
   Show algebraically that, if the radius doubles, the new volume is 4 times the volume of the original.

Save your responses from Try This 2 to your course folder.

 

Share 2

 

Share your responses to the questions in Try This 2 with a classmate or with a group of people. Then discuss the following:

• What is the relationship between changes in the linear dimensions of cylinders and the effect of the changes on volume?
  
  
• How does this relationship compare to the relationship discussed in Share 1?

If required, save a copy of your discussion in your course folder.