Lesson 5

Suppose two three-dimensional objects are similar; that is, one is simply a scale factor of the other. If you know the dimensions of one of the objects, you can determine the dimensions of the other by using the scale factor.

Example

An aquarium manufacturer wishes to scale each dimension of a popular spherical bowl so the bowl has twice the capacity. What scale factor will be used? Round to two decimal places.

Solution

Since the bowls are spheres, changing the radius is equivalent to changing all three dimensions.

The new capacity is two times as large, so the capacity scale factor is 2.

(linear scale factor)3 = capacity scale factor

Let k be the scale factor.

(k)3 = 2

Take the cube root of both sides to eliminate the exponent on k.

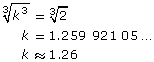
The bowl dimensions will be increased by a scale factor of 1.26 in order to double the capacity of the bowl.

Note: On some calculators you must use the following keystrokes to find a cube root of a number. To find the cube root of 2, press

Self-Check 2

1. The manufacturer of conical paper cups wishes to make a cup that will hold four times the capacity of the best-selling cup. The manufacturer wants to retain the same cup proportions. The company will have to change all dimensions by the same scale factor. What scale factor should be used? Round to two decimal places. Answer
   
   
2. If the diameter of the original cup in question 1 were 6 cm, what would be the diameter of a cup that holds four times as much liquid? Round to the nearest tenth of a centimetre. Answer