Lesson 2

Explore

 

Through your Share discussions, you may have discovered that there are a number of methods to determine whether the truck driver will arrive on time. You may have determined your answer by extending the table of values up to 8 h, by drawing the graph, or by creating and solving a direct linear equation. Regardless of the method you used, it is important that you are able to clearly and confidently support your answer through your shown work.

 

In the Discover activity the graph you constructed should have resembled the following graph:

 

 

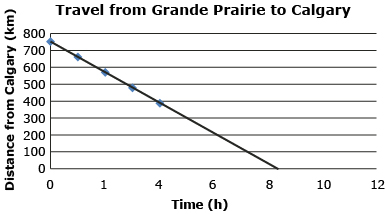
From the graph, you can clearly see the trip will take over 8 h, since the line crosses the x-axis between 8 and 9 h. As a result, you can confidently conclude that the truck will not arrive by 4:00 p.m.

 

To calculate the slope, choose two points on the line; for example (0, 750) and (4, 390). Apply the slope formula.

 

 

Substitute the values for x and y.

 

 

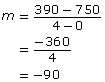
Since the vertical units are kilometres (km), and the horizontal units are hours , the slope is –90 km/h. This value represents the average speed of the truck. The slope is negative because the line is falling to the right (from the graph) or negative because the distance from Calgary is lessening by 90 km for every hour travelled.

 

The y-intercept is 750, and this relates to the initial distance from Grande Prairie to Calgary. In this case the points should be connected. This is because, for every hour or part thereof, the trucker is getting closer to Calgary.

 

Any linear relation can be described by the formula y = mx + b, where (x, y) represents any point on the line, m is the slope, and b is the y-intercept. The above linear relation can then be described as y = −90x + 750.

 

You noted from the graph that it would take over 8 h to make the trip to Calgary. To be more exact you could find the x-intercept, the place where the line touches the horizontal axis and is described by the point (x, 0). Substitute (x, 0) into the equation and solve for x.

 

 

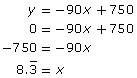
The trip will take or 8 h and 20 min. The driver will arrive at approximately 4:20 p.m.