Lesson 3
1. Lesson 3
1.4. Explore 3
Module 1: Logic and Set Theory
You may have discovered in Try This 2 that the words and, or, and not can be used to describe different areas of a Venn diagram. The intersection of sets A and B can also be described as the set of elements in “A or B.” The union of sets A and B can also be described as the set of elements in “A or B.” The complement of A and B is described as the set of elements “not in A and B.”
Read “Mid-Chapter Review” on pages 36 and 37 of your textbook. Note the use of the words and, or, and not as well as the use of the other set theory terminology.
In the next activity you will see how set theory can be useful for analyzing real-world problems.
Try This 3
Complete “Investigate the Math” questions A, B, C, D, and E on page 22 of your textbook. Creating a Venn diagram in the order described will make it easier to solve this problem. You may also find it useful to work with a partner on this problem.
Save your responses in your course folder.
Share 2
Share your final Venn diagram with a partner. If your diagram differs from the one created by your partner, try to come to agreement on a correct Venn diagram.
If required, save a record of your discussion in your course folder.
The principle of inclusion and exclusion can be extended to solve examples that involve three sets that intersect.
Consider the next scenario. Each member of a sports club plays at least one of the following sports: soccer, rugby, or tennis.
"Nuno Garuti"/Hemera/Thinkstock
The following information is given:
- 163 play tennis.
- 36 play tennis and rugby.
- 13 play tennis and soccer.
- 6 play all three sports.
- 11 play soccer and rugby.
- 208 play rugby or tennis.
- 98 play soccer or rugby.
Use this information to
- draw a Venn diagram
- determine the number of members in the club
A possible solution would be as follows.
- Draw a Venn diagram to represent the club and the three sports.
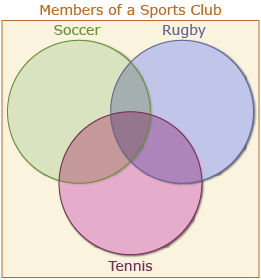
From the information provided, 6 people play all three sports; therefore, you can fill in the middle intersecting part with a 6.
n(S ∩ R ∩ T) = 6
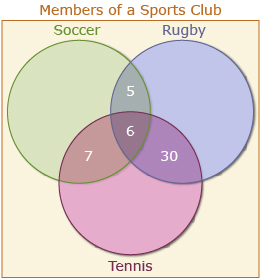
You can also fill in the intersecting regions for two sports.
- 36 play tennis and rugby. (Subtract the 6 from the middle region and n(T ∩ R) = 30.)
- 13 play tennis and soccer. (Subtract the 6 from the middle region n(T ∩ S) = 7.)
- 11 play soccer and rugby. (Subtract the 6 from the middle region n(S ∩ R) = 5.)
Put these numbers into the Venn diagram.
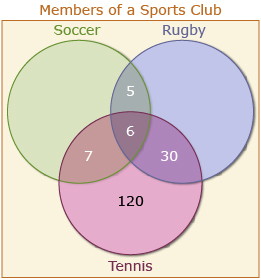
Using the information that 163 play tennis, subtract the other regions in the tennis circle. The outer region is 163 − 6 − 7 − 30 = 120.
Now use the last two pieces of information that tell you about the union of sets to find the remaining regions: 208 play rugby or tennis.
This is the region (R ∪ T). Since all the other regions in these two circles is known, subtract the numbers from 208 to find the outer region in the rugby circle.
208 − 120 − 30 − 5 − 6 − 7 = 40
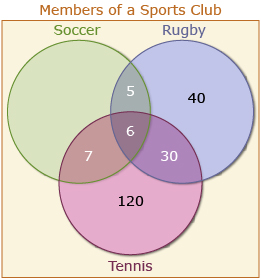
And finally, 98 people play soccer or rugby.
To find the outer region in soccer, you get 98 − 40 − 30 − 5 − 6 − 7 = 10.
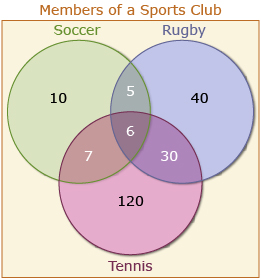
b. Add all the regions up and you find that this sports club has 10 + 5 + 6 + 7 + 40 + 30 + 120 = 218 members.