Lesson 5
1. Lesson 5
1.6. Explore 2
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
You may have found that the questions in Try This 2 could be solved in a similar method to those of the playlist example; however, the number of favourable outcomes in Try This 2 was a bit more complex. Read the following solutions and compare them to your solution.
A winter carnival committee of 6 people needs to be selected from 8 boys and 10 girls.
- Complete the following to determine the probability that the committee will have 3 boys and 3 girls.
First, you were asked to explain if order is important for this question. Order is not important because the positions on the committee are indistinguishable. You can use a process similar to the one shown in the MP3 playlist example. Find the number of favourable outcomes divided by the total number of outcomes.
Then, you were asked to answer a series of questions about outcomes. Following are the solutions.
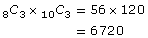
Determine the number of favourable outcomes.
This is the number of ways of choosing 3 boys from 8 boys and 3 girls from 10 girls.
18C6 = 18 564
Determine the number of total outcomes.
This is the number of ways of choosing 6 people from 18 people.
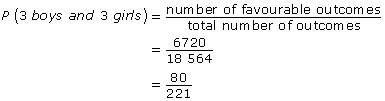
Determine the probability of 3 boys and 3 girls by dividing the number of favourable outcomes by the total number of outcomes.
-

When representing an answer for a probability question, there are three possible ways to write the answer: as a fraction in lowest terms, as a decimal, or as a percentage. So, the answer of
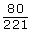 could also be written as 0.362 (rounded) or 36.2%.
could also be written as 0.362 (rounded) or 36.2%.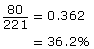
-
What information will be required to calculate the probability that at least 2 members are girls?
To calculate the probability that at least two members are girls, you need to know the total number of possible committees and the number of committees that include at least 2 girls. - Calculate the probability that at least 2 members are girls.
You can solve this using direct reasoning or indirect reasoning.
Method 1: Direct Reasoning
To use direct reasoning, find the total number of different committees that have at least 2 girls and then divide by the total number of committees.
At least 2 girls means there could be 4 boys and 2 girls or 3 boys and 3 girls or 2 boys and 4 girls or 1 boy and 5 girls or 0 boys and 6 girls.
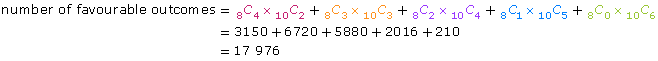
The total number of outcomes is 18C6 = 18 564.
Many calculators include a fraction command that will convert a decimal to a fraction in lowest terms. This command can be used to reduce fractions. To do this, divide the fraction to convert it to a decimal. Use the fraction command to convert it back to a fraction, but now in lowest terms.
You may need to reference your calculator manual or contact your teacher to find out where the fraction command is located on your calculator.
Try using this strategy to simplify the fraction from the problem. You should be able to show
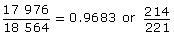
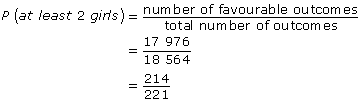
The probability that there will be at least 2 girls on the committee is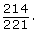
Method 2: Indirect Reasoning
To use indirect reasoning, find the probability of the complement of at least 2 girls and then subtract from 1. This means you find the probability the committee has 0 girls or 1 girl and then subtract this probability from 1.
View the multimedia piece titled Indirect Reasoning to see how Method 2 is used to solve the problem.
Image: iStockphoto/Thinkstock
-
What information will be required to calculate the probability that at least 2 members are girls?
Self-Check 1
- A class of 17 boys and 13 girls is travelling on a bus.
![]()
- Complete questions 2, 3, 5, 8, and 9 from pages 159 and 160 of your textbook. Answer