Lesson 2
1. Lesson 2
1.7. Explore 3
Module 5: Rational Expressions
In Try This 3 you saw that non-permissible values may seem to be different for equivalent rational expressions, but that is not the case. As such, non-permissible values must be identified for the original rational expression, and then those same non-permissible values are applied to any other equivalent expression. Restrictions are important to correctly describe what the rational expression represents. Therefore, restrictions must be included with the simplified product. For example, from Try This 3, you would write the following:
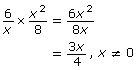
There are two slightly different methods of multiplying and simplifying rational expressions. In the multimedia piece titled Multiplying Rational Expressions, the expressions are first multiplied and then simplified.
In the next example, individual expressions are first simplified and then multiplied together.
Example

Ingram Publishing/Thinkstock
Aki was presented a similar problem, ![]() and had a different idea on how to solve it.
and had a different idea on how to solve it.
First, Aki stated the non-permissible values by looking at the denominators of each fraction.
a ≠ 0
Her next step involved simplifying each individual fraction using prime factorization.
![]()
She then simplified each fraction.
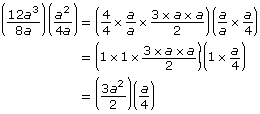
Aki then multiplied the numerators and denominators.
![]()
She then looked for further simplification but noticed there wasn’t any. So her final answer is
![]()
Aki’s solution is just another method of multiplying two rational expressions together.
