Lesson 2

As you saw in Try This 5, dividing rational expressions is similar to dividing rational numbers. One difference is that, in the case of rational expressions, you must state the non-permissible values. In Try This 6 you may have noticed that non-permissible values will occur when a denominator is equal to 0 if the second expression (the divisor) is equal to 0.

 

Watch Dividing Rationals Example, and pay attention to how non-permissible values are determined and how the expression is simplified.

 

 

Now that you have navigated through the example, try simplifying the following expression. Remember to state the restrictions of the expression.

 

 

The following instructions will guide you through this solution.

 

Step 1: Factor each expression.

 

 

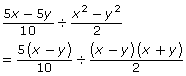
Step 2: State non-permissible values. (Remember to consider both the numerator and denominator of the divisor—the second term of the expression.)

 

 

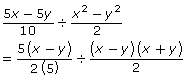
Since the numerator of the divisor will equal 0 if x − y = 0 or x + y = 0, the non-permissible values are x = y and x = − y.

 

Step 3: Change the division statement into a multiplication statement (i.e., multiply by the reciprocal).

 

 

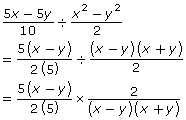
Step 4: Reduce the expression by factoring out any common factors.

 

 

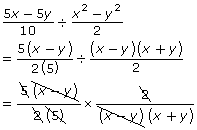
Step 5: Write the simplified expression. Remember to include the non-permissible values.

 

---

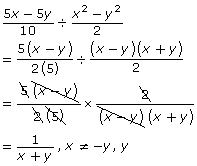
When simplifying rational expressions, you need to apply strategies learned Lessons 1 and 2. Dividing Rational Expressions: Difficult Example shows another example of dividing rational expressions.

 

 

Self-Check 3