Lesson 3

Discover

 

To add and subtract rational numbers, you often have to find the lowest common multiple (LCM) in order to create equivalent fractions that have the same denominators. In this section you will explore two different methods of determining the lowest common multiple for a set of rational expressions.

 

Try This 1

 

Method 1: Finding the LCM Using the Factored Form

1. Complete a table like the one shown. The first row has been completed to give you an idea of what is expected.
   
   

   Polynomials	Factored Form	LCM
   x2 2x
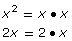
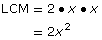
   10xy2 4x2y
   6x 4x2 x3
   8(a + b)3 4(a2 − b2)

 

Method 2: Finding the LCM Using Product and GCF

2.  
   1. Discover an alternate method of finding the LCM by completing a table like the one shown and then answering the questions that follow. In the table, treat binomials as a single factor. Do not expand (multiply out) any of the factors. The first row has been completed to give you an idea of what is expected.
      
      

      Expressions	Product	GCF	LCM	GCF • LCM
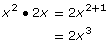
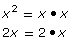
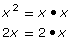
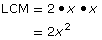
      x2 2x		GCF = x		x • 2x2 = 2x3
      12xy 15y2
      (y + 2) 2(y + 2)
      (x + 3) (x − 3)

   2. Look at the rows of your completed table. Do you notice any patterns as you look horizontally across the rows? From these patterns, do you see another method you could use to find the LCM?
3. What other previous math concepts have you learned that required you to work with lowest common multiples?
4. Why do you think it is important to be able to have different strategies to determine the LCM of a set of expressions?

Save your responses in your course folder.