Lesson 3

In Try This 3 you may have seen that adding and subtracting rational expressions with common denominators is very similar to adding and subtracting rational numbers. Compare what you did in Try This 3 with the example of adding rational numbers with the following common denominators. How does your method compare?

State the non-permissible values of the rational expression by looking at the denominators.
Write the two rational expressions as one expression with the common denominator x − 3.
Simplify the numerator, and state the non-permissible value to the final answer.
Verify your answer.	Plot 1  Plot 2  Plot 3 Y1 = (4x) / (x − 3) + (x − 2) / (x − 3) Y2 = (5x − 2) / (x − 3) Y3 = Y4 = Y5 = Y6 =   X Y1 Y2 −3 −2 −1 0 1 2 3 2.8333 2.4 1.75 .66667 −1.5 −8 ERROR 2.8333 2.4 1.75 .66667 −1.5 −8 ERROR

The following example shows how to prevent a common error that occurs when evaluating rational expressions in subtraction. Pay attention to how parentheses are used to keep the binomials in the numerator separated to start and how this expression is then simplified.

Example

Verification

Consider another example. Notice that, before simplifying, the denominator of the sum is the same as the denominator of the original rational expressions. Also pay attention to how factoring is used to simplify the expression.

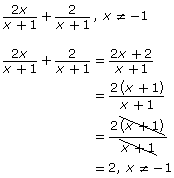
Why is there still a restriction placed on the solution?

Why were no parentheses shown in the second line of this solution? When are they necessary?

Self-Check 1