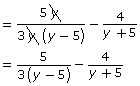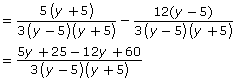1. Lesson 3

1.13. Explore 9

Mathematics 30-2 Module 5

Module 5: Rational Expressions

 

In Try This 6 you learned that there are times when you need to factor the rational expression before determining the LCD. Look at another example.

 

Simplify.

The first step is to always state the non-permissible value.

 

You will need to factor in order to find the values of y that will restrict the expression.

 

Therefore, the restrictions are y ≠ 0, 5, −5.

Next, find the LCD.

 

Simplify the first expression by cancelling the 1 of .

 

The LCD equals 3(y − 5)(y + 5).


Multiply each expression by a fraction that is equal to 1 so each ends up with the denominator 3(y − 5)(y + 5).

Now each denominator is the same. Simplify.

Subtract the numerators.

Make sure to include the restrictions from the original expressions.



textbook

To see another example of factoring, read “Example 4” on pages 247 and 248 of your textbook. Notice when factoring is used to help add the rational expressions.

 

Try This 7

 

Complete Adding Rationals. This example is similar to “Example 4” that you just read in the textbook. After you complete the multimedia piece, answer the questions that follow.

 

 

This is a play button for Adding Rationals.

  1. Why was the denominator of the first rational expression factored before a common denominator was determined?
  2. Why was it necessary to factor the numerator when trying to simplify
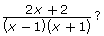
  3. Why is −1 included as a non-permissible value for the final expression 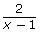when −1 does not make the denominator zero?

course folder Save your work in your course folder.

 

Self-Check 3
  1. Complete Adding and Subtracting Rational Expressions Self-Check: Unlike Denominators.

     
    This is a play button for Adding and Subtracting Rational Expressions Self-Check: Unlike Denominators.

 

textbook


  1. Complete questions 1.d., 5.a., 5.b., 7, 8, and 9 on pages 249 and 250 of the textbook. Answers