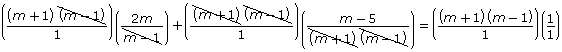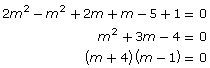Lesson 4
1. Lesson 4
1.9. Explore 5
Module 5: Rational Expressions
The steps you used in Try This 4 may have been similar to the steps shown in the following example. After reviewing the example, think about any changes you might want to make to your solution in Try This 4.
Solve ![]()
Factor. |
|
Determine the non‑permissible values. |
m ≠ ±1 |
Find the LCD. |
LCD = (m − 1)(m + 1) |
Multiply each term on both sides of the equation by the LCD, and cancel common factors. |
|
Multiply the remaining rational expressions. |
|
Since this is a quadratic equation, manipulate the equation by bringing all terms to one side and solve by factoring. |
|
The solutions are m = −4 or m = 1. Check to see if the solutions are extraneous. Since one of the non-permissible values is 1, m = 1 is extraneous. |
Therefore, the only solution is m = −4. |
If you feel you need additional help, review “Example 2” on page 254 of your textbook. In this example, Marlene solves the equation, but the answer is a non-permissible value, which means there is no solution. The example should remind you to be aware of solutions that can’t be used since they are non-permissible. These solutions are called extraneous roots.
Self-Check 2
Complete questions 4, 5, and 6 on page 258 of your textbook. Answers
Add the following terms to your copy of Glossary Terms:
- rational equation
- extraneous root