Lesson 5
1. Lesson 5
1.4. Discover
Module 5: Rational Expressions
Discover

iStockphoto/Thinkstock
The first event at Super Challenge Day is Scooter Rendezvous. Scooters have long represented a fun and economical way of travelling. Not all scooters are built the same. Some scooters have larger engines, others have more storage room, and all have unique designs.
In Scooter Rendezvous, team members start at opposite ends of a 50-km stretch of highway. Each team member drives toward the other. The event is completed when the scooters meet. The time it takes each team to complete the event is recorded, and winners are declared based on the fastest times.
Try This 1
Karim and Chandelle participated in Scooter Rendezvous. Karim drove his scooter at an average speed of 60 km/h. Chandelle drove her scooter at an average speed of 90 km/h.
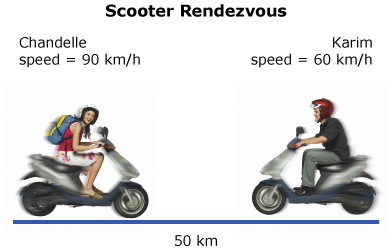
scooters: George Doyle/Stockbyte/Thinkstock
- Use the diagram to help you place the information from the question into a chart like the following. Where a quantity is unknown, use a variable or expression.
Distance (km)
Speed (km/h)
Karim
Chandelle

- If Karim and Chandelle start the race at the exact same time, what do you know about the time it took each of them to arrive at the rendezvous point?
- Choose a strategy that you could use to determine the distance travelled by each driver. Ask yourself these questions if you get stuck:
- What is an algebraic strategy I could use?

- What is a second strategy that I can use?

- What is an algebraic strategy I could use?
![]() Save your work in your course folder. You will revisit these results later in the lesson.
Save your work in your course folder. You will revisit these results later in the lesson.