Lesson 5

Explore

Consider the following types of problems:

• If you could shovel your driveway in 30 min and your friend could do the same job in 25 min, how long would it take both of you to do the job together?
• How much time do you actually save on a 60-km drive if you drive 15 km/h over the speed limit?
• What amount of floor cleaner do you have to add to a bucket containing 10 L of water to create a solution that is 5% floor cleaner?

 

These types of problems can be solved using rational equations. In fact, rational equations can be used to model and solve many problems related to work, motion, and proportions.

 

Problem solving is perceived as being difficult by some students. Here are some strategies to help with application-type questions:

• Strategy 1: Look for key words in the problem.
• Strategy 2: Make a table or an organized list.
• Strategy 3: Draw a picture or a graph.
• Strategy 4: Look for patterns.
• Strategy 5: Work backwards.
• Strategy 6: Guess and check.

Using the six strategies, you will focus on three particular types of applications that involve rational equations: work problems, motion problems, and proportion problems.

 

Solving a word problem can be challenging, but doing so does not have to be difficult. Careful reading, proper planning, and a good understanding of mathematics are keys to success in modelling and solving word problems.

 

In Discover, you had to determine the distance travelled by each scooter. You organized your information in a table. It should look similar to the table shown.

 

	Distance (km)	Speed (km/h)
Karim	d	60
Chandelle	50 − d	90

 

You can use the organized information to determine an expression for the time taken by each person to complete his or her portion of the event.

 

Recall that time is equal to the ratio of the distance travelled divided by the speed, or The expressions for the time taken by Karim and Chandelle to complete the event are shown in the table.

 

	Distance (km)	Speed (km/h)	Time
Karim	d	60
Chandelle	50 − d	90

 

Since Karim and Chandelle start and stop driving at the same time (i.e., when the scooters meet), their time travelled should be identical. In other words, Karim’s time = Chandelle’s time.

 

Substitute the expressions that represent time from the table above to get the following rational equation.

 

 

Try This 2

1. Solve the equation 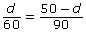 for d. How far did Karim travel? How far did Chandelle travel?
2. Compare your answers to those you determined in Try This 1 question 3. Are your answers the same?
3. How much time did it take for Karim and Chandelle to complete the event?

Save your responses in your course folder.

 

Share 1

 

Work with a partner or a group to complete the following questions.

1. How can you check to see if your answers are correct?
2. Did you check for extraneous solutions?

If required, save a record of your discussion in your course folder.