Lesson 5
1. Lesson 5
1.7. Explore 3
Module 5: Rational Expressions

Hemera/Thinkstock
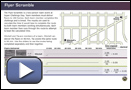
Another event at Super Challenge Day is the Flyer Scramble. Flyers are a great way to let people know about community events, new businesses, and missing pets.
In this event, teams of two must deliver flyers to 100 homes. Flyers must be placed inside mailboxes, and team members must only use walkways. Each team member completes the challenge and is timed. The results are used to calculate the time it would take to complete the route by both team members working simultaneously.
Each team member then runs through the route to attempt to beat the calculated time. The winning team is the team with the fastest actual recorded or calculated time.
Try This 3
Mitchell and Tia are members of a team participating in the Flyer Scramble event. Mitchell can deliver the flyers in 40 min. Tia covers the same route in 50 min. Open up the Flyer Scrambler applet that shows the routes being completed separately and then together.
Now that you have played with the applet, answer the following questions based on your observations.
- Determine the fraction of the flyers Mitchell could deliver in
- 10 min
- 20 min
- 40 min
- What fraction of the flyers could Mitchell deliver in t min? How did you determine this?
- Determine the fraction of the flyers Tia could deliver in
- 10 min
- 20 min
- 50 min
- What fraction of the flyers could Tia deliver in t min? How did you determine this?
- What does the fraction
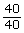 mean for Mitchell?
mean for Mitchell?
- The applet shows that it takes Mitchell and Tia approximately 22.2 min to complete the route together. The rational equation that represents the time it takes both Mitchell and Tia to complete the route is
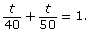
- What does the expression
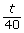 represent?
represent? - What does the expression
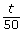 represent?
represent? - When you add the two fractions together, why do they equal 1?

- Verify that the time it would take Tia and Mitchell working together is 22.2 min.
- What does the expression
Share 2
Work with a partner to complete the following questions.
- The average time between Tia and Mitchell is 45 min. Why would this not be the answer to the problem?
- What if Mitchell did the route in 38 min (which is 2 min quicker than he is doing it now) and Tia did it in 52 min (which is 2 min slower than she is doing it now)? Would they still do the route together in 22.2 min? Explain your estimation.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.