Lesson 1

In Try This 3 you may have found the relationships between the a and b parameters of the function and the corresponding graph of exponential functions in the form y = a(b)x, where a > 0, b > 0, and b ≠ 1. These relationships are shown in the following table.

 

Parameter	Effect on Graph
a	equal to y-intercept
b	If b > 1, the function is increasing.   If 0 < b < 1, the function is decreasing.

 

Consider the function y = 2(5)x, where a = 2 and b = 5. You know this will be an increasing function because b > 1.

 

Confirm that there is no x-intercept:

• Let y = 0; therefore, 0 = 2(5)x. From this, determine an x-value that will result in the function becoming 0.
• There is no value of x that results in the function becoming 0; therefore, there is no x-intercept.

The y-intercept is the a-value; confirm that this is the case:

• Let x = 0; therefore,
  
  
   
  

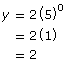
• The y-intercept is 2, which is the a-value.

Because the b-value is greater than 1, this function’s end behaviour is increasing from quadrant II to quadrant I.

 

The domain of this function is {x|x ∈ R}, which means that any value of x can be used. This makes sense as the graph goes from quadrant II to quadrant I, which encompasses all of the x-axis.

 

The range of this function is {y > 0, y ∈ R}, which means that only positive values of y can be used. This makes sense as the function is above the x-axis and does not touch the x-axis.

 

You can verify these characteristics by graphing the exponential function y = 2(5)x.

 

 

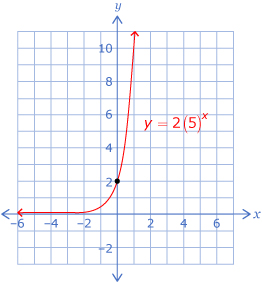
From the graph, note the following:

• The graph never touches the x-axis; therefore, there is no x-intercept.
• The y-intercept is 2.
• The end behaviour is from quadrant II to quadrant I; the graph is increasing.
• The domain is {x|x ∈ R}.
• The range is {y|y > 0, y ∈ R}.