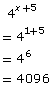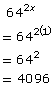Lesson 2

In Try This 2 you found that rewriting the powers on both sides of the equation to have the same base allowed you to determine the unknown variable in the exponent(s). If two powers are equal and their bases are equal, their exponents must also be equal. This can be expressed by the property that if bx = by, then x = y and b ≠ −1, 0, 1.

To use this property to solve exponential equations, there must be only one power on each side of the equation and the bases of the powers must be the same.

Acceptable (Each side has one power and both powers have the same base.)	Not Acceptable (Each side of the equation must have one power.)	Not Acceptable (Bases must be the same on each side of the equation.)

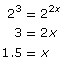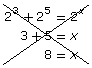Sometimes, in order to change the base of a power, you must remember how to apply the exponent laws.

For example, in Try This 2 you solved 4x + 5 = 642x.

Verify your solution by substituting the value for x into the original equation.

When entering powers into your calculator, use brackets around the exponent; for example, to enter 32x − 3 into your calculator, type 3, ^, (, 2, x, −, 3, ). Note that some calculators use xy to label the exponent button. Also, remember to be careful with negative values: (−2)^4 is different from −(2)^4.

The solution is x = 1.