Lesson 3

Explore

 

In Try This 1, in order to solve for the magnitude, y, given the amplitude, x, is 1, the logarithmic notation would be y = log10 1. Using your calculator you determined the answer is 0.

 

In Try This 1 you also saw that very large amplitudes could be described using much simpler, smaller numbers by taking the logarithms. Comparing earthquakes using the Richter scale numbers of 0, 1, 2, and so on is much simpler than comparing the amplitude numbers of 1, 10, 100, and so on. Think about how large some of the numbers on the following diagram would be if logarithms were not used.

 

From PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission. top photo: iStockphoto/Thinkstock; bottom photo: Stocktrek Images/Thinkstock

 

You may have also noticed a relationship between logarithms and exponents. In Try This 1 the value of the exponent was the same as the logarithm. Notice that the base of the exponent is the same as the base of the logarithm. In fact, a logarithm is an exponent.

 

 

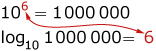
Using a more formal definition, a logarithm of a number is the exponent by which the base has to be raised to produce that number. The base of a logarithm is usually written as a small number. Bases other than 10 can be used, such as 3 in the diagram that follows.

 

 

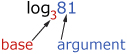
Logarithms have two parts to them. The small number is called the base and the large number is called the argument. Logarithms like this represent real numbers; for example, log3 81 = 4.