1. Lesson 4

1.3. Explore 2

Mathematics 30-2 Module 7

Module 7: Exponents and Logarithms

 

In Try This 2 you noticed that the graph of y = log10 x is identical to the graph of x = 10y; therefore, the characteristics of the two graphs are the same.

 

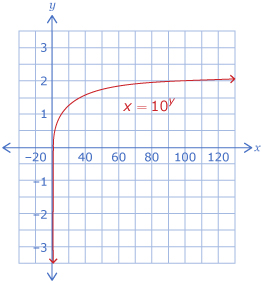
This is a graph of x equals 10 to the power of y. It starts in quadrant IV and ends in quadrant I.
 
 
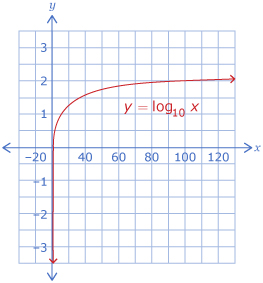
This is a graph of y equals the base 10 logarithm of x. It starts in quadrant IV and ends in quadrant I.



 
Characteristics y = log10 x
Domain x > 0
Range y ∈ R
x-intercept The x-intercept value is 1.
y-intercept none
End behaviour from quadrant IV to quadrant I

 

Now that you are familiar with the characteristics of the graph of y = log10 x, you will examine how a change to the parameter a affects the graph of y = a log10 x, where a is a real number.

  

Try This 3

 

Open the Logarithmic Functions applet.

 

 

This is a play button for Logarithmic Functions.

  1. Investigate the effects of a on the graph of y = a log10 x by moving the slider. Record your results in a table similar to the following.

    Characteristics a < 0 a > 0
    Value of x-intercept    
    Value of y-intercept    
    Domain    
    Range    
    End Behaviour    
    1. How could knowing the a-value help you predict the characteristics of the graph of y = a log10 x?
    2. Based on your answer to 2.a., predict what the graph of y = −8 log10 x will look like. Check your prediction using the Logarithmic Functions applet.
course folder Save your responses in your course folder.