Lesson 5

Read “Example 1” on pages 443 and 444 of your textbook to see a numeric example of the relationships described in the table.

 

The product and quotient laws of logarithms can be used to manipulate an expression into a different form. The following examples show how two logarithms can be combined into a single logarithm.

 

log7 6 + log7 9	The logarithms have the same base, so they can be combined.
= log7(6 × 9)	The logarithms are added, so use the product law of logarithms, logb (M × N) = logb M + logb N.
= log7 54	Determine the product and write a single logarithm.

 

log3 72 − log3 8	The logarithms have the same base, so they can be combined.
	The logarithms are subtracted, so use the quotient law of logarithms,
= log3 9	Determine the quotient and write a single logarithm.
= 2	This logarithm can be evaluated to a whole number.

The process shown in the examples can be reversed to write a logarithm as two separate logarithms, as shown in the following examples:

 

log5 (8 × 12) = log5 8 + log5 12

 

 

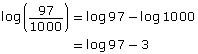
Self-Check 1

1. 
   
   1. Complete “Your Turn” at the end of “Example 1” on page 444 of your textbook. Answer
   2. Complete “Your Turn” at the end of “Example 2” on page 444 of your textbook. Answer
   3. Complete “Your Turn” on page 445 of your textbook. Answer
2. Complete questions 1.a., 2.b., 3.a., 4.b., 6.b, 6.c., 8.b., and 14 on pages 446 and 447 of your textbook. Answer